Construct Interactive Voronoi Edges In TypeScript and Canvas
Click and drag to move the rotating box around the Voronoi diagram
Introduction
The goal of this project was to generate Voronoi diagrams such that I could use the edges of the diagram as interactive roads. I started down this path because I am interested in making a driving game where the roads are randomly generated, and I learned from this video by Herbert Wolverson that Voronoi Diagrams is one way to do it. While there are already JavaScript libraries that can generate Voronoi diagrams, I wanted to code this up from scratch for two reasons: 1) to learn the algorithm and 2) to keep the file size small since I intend to use this on a JS13k gamejam.
In the canvas above, you can click and drag to move the spinning square. When the square overlaps an edge, the edge will turn blue. The red line represents the size of the overlap.
If you’d like to try this out on a separate page, here’s the link. If you’re interested in this code, here’s the GitHub repo.
What is a Voronoi Diagram
A Voronoi diagram partitions a plane into regions. These regions are divided so that every point within a given region is closest to a “seed” point. This becomes clearer by looking at a diagram:
The different colored polygons are regions and the block dots are seeds. (Image from Wikipedia)
Steps
One note is that there is a simpler way to create Voronoi diagrams if you don’t need the edges to be their own objects. This may be the case if you are more interested in the visuals than you are in interacting with the edges. This Coding Train video shows this simpler algorithm, albeit with Worley Noise instead of Voronoi diagrams.
However, to be able to handle collision detection, we need each road to be its own object and therefore we can’t go pixel by pixel as described in the Coding Train video. The process I followed was pulled from a few blog posts and videos, notably this post at Gorilla Sun and this video by Scott Anderson.
There are a lot of steps in the process, but the high level outline goes like this:
- Generate the Delaunay triangulation of a set of points
- Convert the Delaunay triangles to a set of edges of a Voronoi diagram
- Convert the Voronoi edges to roads
In the end, everything is chained together like this:
const roads = voronoiEdgesOfDelaunayTriangles(triangulate(points)).map((edge) => roadFromEdge(edge));
On to the first step!
Generate Delaunay Triangulation
Googling around, it appears the most straightforward way to generate a Voronoi diagram is to first generate a Delaunay triangulation and then convert that to a Voronoi diagram.
A Delaunay triangulation is a set of triangles where no point is within the circumcircle of any triangle. A circumcircle is a circle that passes through all three vertices of a triangle. In other words, the Delaunay triangulation generates triangles, and all the “seed” points should be verticies in those triangles. Like a lot of this stuff, the idea is easier to understand by looking at a picture:
Note that all the circles go through the vertices of the triangles, and no points lie within any circle.
(Image from Wikipedia)
How to Generate a Delaunay triangulation
To make matters more confusing, there are multiple ways to generate a Delauney triangulation. The simplest method seems to be the Bowyer-Watson algorithm. Other links in this post describe that algorithm better than I will, so I will just run through the code.
For starters, here are the interfaces for points, triangles, and circles:
export interface IPoint {
x: number;
y: number;
}
export interface IEdge {
v0: IPoint;
v1: IPoint;
}
interface ICircle {
center: IPoint;
radius: number;
}
interface ITriangle {
v0: IPoint;
v1: IPoint;
v2: IPoint;
}
interface ITriangleInTriangulation extends ITriangle{
circumcircle: ICircle;
neighbors: ITriangleInTriangulation[];
}
The triangulate method takes seeds points and returns an array of triangles in the triangulation:
// Pulled a lot of this from
// https://www.gorillasun.de/blog/bowyer-watson-algorithm-for-delaunay-triangulation/#the-super-triangle
function triangulate(vertices: IPoint[]): ITriangleInTriangulation[] {
// Create bounding 'super' triangle
const superTriangle = circumscribingTriangle(circleFromPoints(vertices));
const superDelaunayTriangle = { circumcircle: circumcircleOfTriangle(superTriangle), neighbors: [], ...superTriangle};
// Initialize triangles while adding bounding triangle
let triangles: ITriangleInTriangulation[] = [superDelaunayTriangle];
// Add each vertex to the triangulation
vertices.forEach((vertex) => {
triangles = addVertexToTriangulation(vertex, triangles);
});
return triangles;
};
The steps here are as follows:
- Create a super triangle of the points
- Iterate through each point and add it to the trianglulation, following the Bowyer-Watson algorithm
To get started, we need to create the initial super triangle. This is done by creating a circle that contains all the points and then creating a triangle that contains that circle. Here’s a picture of what we’ll generate:
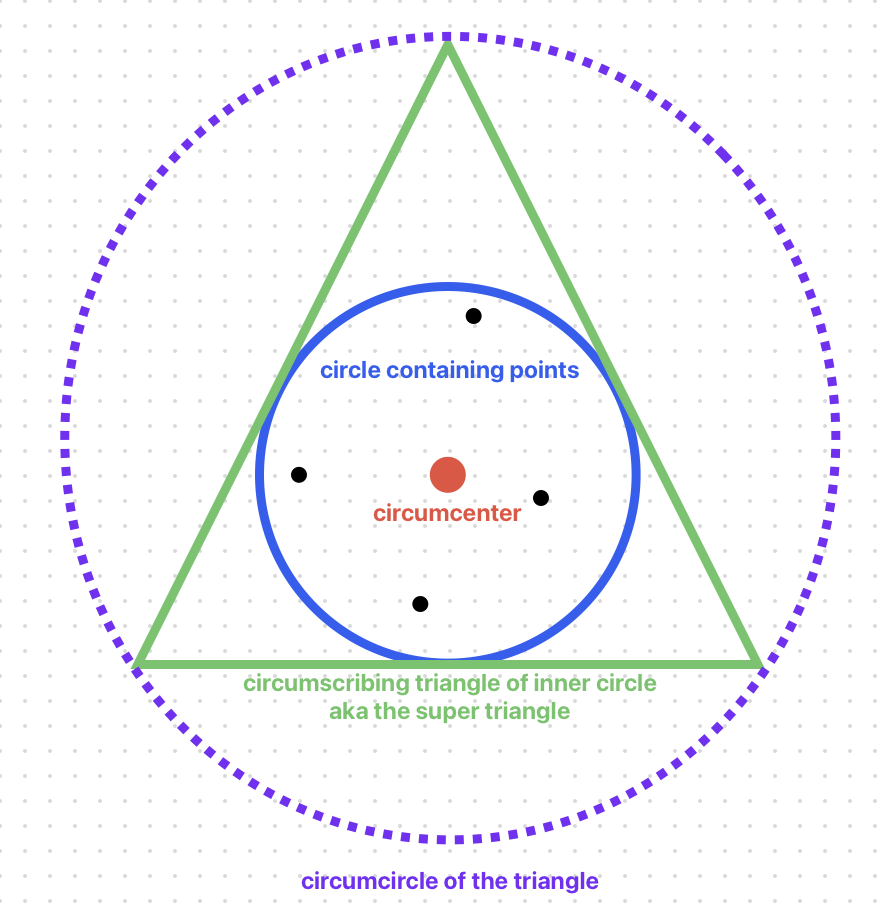
Genreate the Initial Super Triangle
First, we create a circle that contains all the points. Next, create a circumscribing triangle that contains the circle.
The Circle
The center of the circle is the average of all the points, and the radius is the distance from the center to the furthest point. Here’s the code:
function circleFromPoints(points: IPoint[]): ICircle {
const center = points.reduce((sum, point) => ({ x: sum.x + point.x, y: sum.y + point.y }), { x: 0, y: 0 });
center.x /= points.length;
center.y /= points.length;
const radius = points.reduce((max, point) => Math.max(max, distanceBetweenPoints(center, point)), 0);
return { center, radius };
}
The Circumscribing Triangle
With the circle created, we can now create a triangle that contains the circle. This video describes how to calculate the relationship between a triangle and the circle that is inscribed within the triangle. In short, we can use the fact that bisecting the angle of an equilateral triangle creates a 30-60-90 triangle, which is then used to calculate the length of the side of the larger equilateral triangle. Here’s an image describing the relationships:
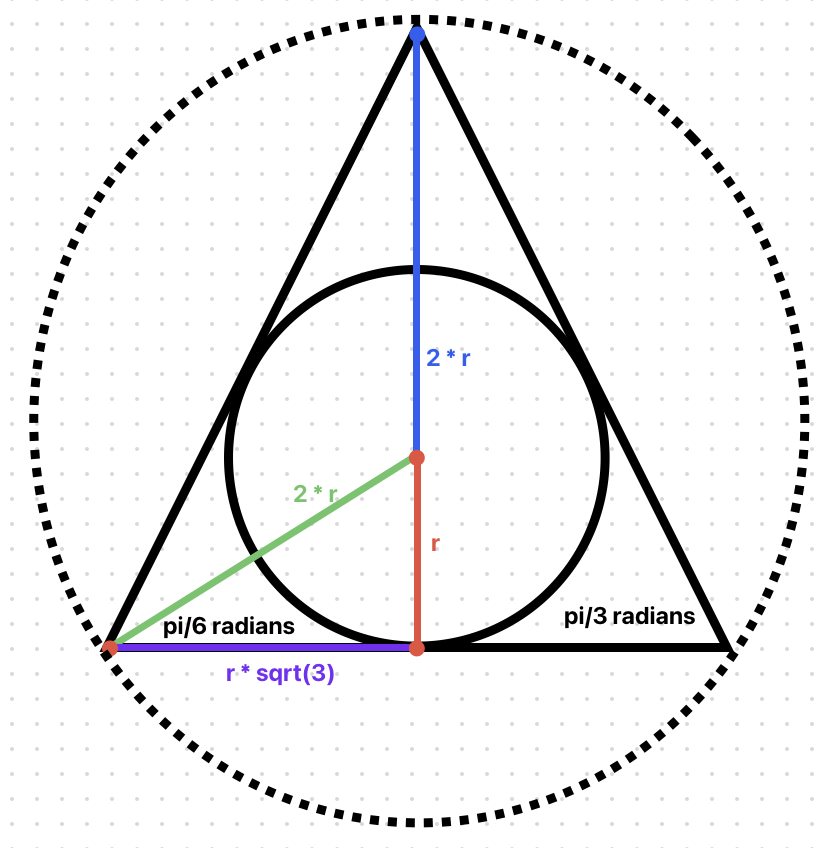
And here’s the code:
// Create a triangle that contains the circle using 30-60-90 triangle rules: https://www.youtube.com/watch?v=mulFsXCBw80
// Note that the video above has a mistake (the half side is r * sqrt(3) not r * sqrt(2))
function circumscribingTriangle(circle: ICircle): ITriangle {
let { center, radius } = circle;
// Calculate the bottom side of the 30-60-90 triangle, which is half the length of the side of the equilateral triangle
const side = radius * Math.sqrt(3);
// Calculate the hypotenuse of the 30-60-90 triangle, which is the radius of the circumcircle of the equilateral triangle
const hypotenuse = radius * 2;
// Top
const v0 = {
x: center.x,
y: center.y + hypotenuse
};
// Left bottom
const v1 = {
x: center.x - side,
y: center.y - radius
};
// Right bottom
const v2 = {
x: center.x + side,
y: center.y - radius
};
return { v0, v1, v2 };
}
Add Each Vertex to the Triangulation
Once we have the initial super triangle, we go through each vertex, adding it to the array of triangles as part of the incremental Bowyer-Watson algorithm.
The code to add the vertex to the triangulation is here:
function addVertexToTriangulation(vertex: IPoint, triangles: ITriangleInTriangulation[]): ITriangleInTriangulation[] {
let edges = [];
// Remove triangles with circumcircles containing the vertex
const trianglesToKeep = triangles.filter((triangle) => {
if (isPointInCircumcircle(vertex, triangle)) {
// Add edges of removed triangle to edge list
edges.push({v0: triangle.v0, v1: triangle.v1});
edges.push({v0: triangle.v1, v1: triangle.v2});
edges.push({v0: triangle.v2, v1: triangle.v0});
return false;
}
return true;
});
// Get unique edges
edges = uniqueEdges(edges);
// Create new triangles from the unique edges of the removed triangles and the new vertex
edges.forEach(function(edge) {
const circumcircle = circumcircleOfTriangle({v0: edge.v0, v1: edge.v1, v2: vertex});
trianglesToKeep.push({ v0: edge.v0, v1: edge.v1, v2: vertex, circumcircle, neighbors: []});
});
return trianglesToKeep;
};
The filter step removes all the triangles that contain the vertex in their circumcircle. The edges from the removed triangles are then added to the edge list, which is filtered to remove duplicate edges. Finally, new triangles are created from the points of each edge combined with the vertex passed in. These triangles are added to the list of triangles and returned.
After running through all the vertices, a complete Delauney triangulation will be generated. A sigh of relief is breathed.
Convert Delaunay Triangles to Voronoi Edges
Now that we have a Delaunay triangulation, we can convert it to a Voronoi diagram. This is done by first creating vertices at the circumcenters of each triangle. The circumcenter is the center of the circumcircle of the triangle.
For each triangle in the Delaunay triangulation, we find the neighboring triangles and create an edge between the circumcenters of the triangles. This Cartography Playground page has some good interactive demonstrations to see how this works.
Here’s the code:
function voronoiEdgesOfDelaunayTriangles(triangles: ITriangleInTriangulation[]): IEdge[] {
// calculate neighbors on each triangle
for (const triangle of triangles) {
const neighbors = neighborDelaunayTriangles(triangle, triangles);
triangle.neighbors = [...neighbors];
}
const voronoiEdges: IEdge[] = [];
for (const triangle of triangles) {
for (const neighbor of triangle.neighbors) {
const triangleCenter = triangle.circumcircle.center;
const neighborCenter = neighbor.circumcircle.center;
const edge: IEdge = { v0: triangleCenter, v1: neighborCenter };
if (!edgeListContainsEdge(voronoiEdges, edge)) voronoiEdges.push(edge);
}
}
return voronoiEdges;
}
Convert the Voronoi Edges to Roads
The great news is that at this point we have done the hard part of creating the Voronoi diagram. The rest is just converting each edge to an interactive road. The Road class is in another file, which you can check out in the repo.
function roadFromEdge(edge: IEdge): Road {
const dx = edge.v1.x - edge.v0.x;
const dy = edge.v1.y - edge.v0.y;
const angle = Math.atan2(dy, dx) + Math.PI/2;
const height = Math.hypot(dx, dy);
// calculate the middle pos
const middlePos = { x: edge.v0.x + dx / 2, y: edge.v0.y + dy / 2 };
// calculate the top left pos
const pos = { x: middlePos.x - ROAD_WIDTH / 2, y: middlePos.y - height / 2 };
return new Road(pos, { x: ROAD_WIDTH, y: height }, angle);
}
Conclusion
And that’s it for generating the Voronoi edges. The rest of the code renders the roads, handles player input and collisions, etc. The collision detection uses the Separating Axis Theorem as described in this Pikuma video.